Cache-aware prefetch details

#1

Hi,

I’m interested in the cache-aware prefetch algorithm mentioned in section 4.2 of the xgboost paper. I’m new to computer architecture and high-performance computing. I’ve tried to figure it out myself for many days but still don’t have an answer, so I hope to get some help here.

I assume the relative code is in https://github.com/dmlc/xgboost/blob/2fcc4f2886340e66e988688473a73d2c46525630/src/tree/updater_colmaker.cc#L381-L398:

      int i;
      const Entry *it;
      const int align_step = d_step * kBuffer;
      // internal cached loop
      for (it = begin; it != align_end; it += align_step) {
        const Entry *p;
        for (i = 0, p = it; i < kBuffer; ++i, p += d_step) {
          buf_position[i] = position_[p->index];
          buf_gpair[i] = gpair[p->index];
        }
        for (i = 0, p = it; i < kBuffer; ++i, p += d_step) {
          const int nid = buf_position[i];
          if (nid < 0 || !interaction_constraints_.Query(nid, fid)) { continue; }
          this->UpdateEnumeration(nid, buf_gpair[i],
                                  p->fvalue, d_step,
                                  fid, c, temp, evaluator);
        }
      }

I understand that cache miss rate would be high when the values do not fit into the cache and they are stored in non-contiguous memory locations. By using the buffer buf_gpair, the values will then be fetched in a continuous way. What I don’t understand is the loop is still going over gpair one by one, wouldn’t it creates the same amount of cache misses?

The paper mentioned a naive implementation of split enumeration introduces immediate read/write dependency between the accumulation and the non-continuous memory fetch operation.

I also found an early presentation suggest use prefetch to change the dependency to long range.
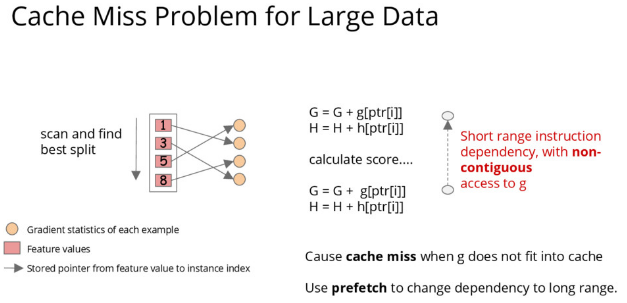
Selection_041

I have no ideas about the dependency impact here. Could anyone help me to understand the benefit of using the buffer? Really appreciate it!

Thanks,

JJ

#2

You may consider writing an e-mail to the original author of the XGBoost paper (Tianqi Chen).

No, because buf_gpair is being used multiple times in the split enumeration loop, so it is worthwhile to reorder the layout with a one time cost to achieve saving down the road.

#3

Thank you Philip. Seems the buf_pair just has 32 elements that is called once for each batch of 32 elements, and one needs to replace the entire buffer for the next 32-element batch every time.

I will also reach out to the author.

#4

It is still worthwhile to replace the buffer buf_gpair. The cost of filling buf_gpair is more than offset by the speedup achieved by better data locality in UpdateEnumeration(). Memory accesses have drastically different performance cost depending on how they are ordered. You still have to fetch the same number of gradient pairs from gpair, but by reordering the accesses (via buf_gpair), the accesses are now faster.

This is because of the memory hierarchy in modern computers. I suggest that you study the case of optimizing matrix multiplication. You can achieve 2x speedup by reorganizing matrix multiplication with blocks, such that each block would fit into the L1 cache.

#5

Thanks for your reply!

Yes, I’m aware of the spatial locality. So for each element, they will be fetched once regardless of using the buffer or not. The difference is the naive way fetched them directly to UpdateEnumeration(). I guess what you are saying is the cost of filling the buffer then do the update is much less than read the data and immediately use it to accumulate. To me, the only difference is the latter case has a shorter dependency between the accumulation and the non-continuous memory fetch operation as described in the paper. The remaining question for me now is just why this short dependency will cause the slowdown. Do you have any insights? Thanks a lot.

#6

Precisely. This is because of spatial locality. We cache gradient pairs in buf_gpairs which is guaranteed to fit inside the L1 memory cache, and subsequent random accesses to buf_gpairs are very fast.

Both dependency and spacial locality contribute to performance speedup.

  1. Spacial locality
    It is worthwhile to cache gradient pairs into buf_gpairs (which fits inside the L1 cache) as we will then access the gradient pairs multiple times inside UpdateEnumeration. As long as UpdateEnumeration() accesses each gradient pair more than once, we come out ahead.

  2. Dependency
    By batching multiple gradient pairs into buf_gpairs prior to calling UpdateEnumeration, we enable instruction-level parallelism (ILP) inside UpdateEnumeration: multiple read/writes that do not depend on each other can take place simultaneously. Most modern processors are superscalar processors that are capable to executing multiple instructions per cycle.

#7

Thanks for the pointer to ILP, leading me to some tutorials regarding ILP and instruction pipeline. I think the data dependency (read after write, hope it is what the paper referred to) is still in the update function, as we are accumulating the sum one by one. However, there will be no stall as we already have the values in the cache using the buffer. The buffer filling step does consist of independent data load and save. Does this reasoning make sense? Sorry, this is new stuff to me but certainly learnt a lot.