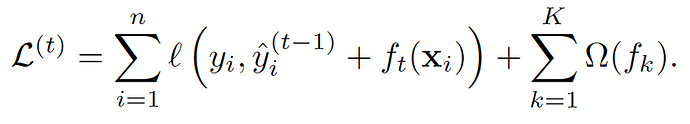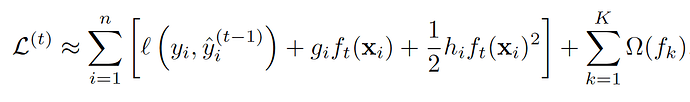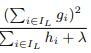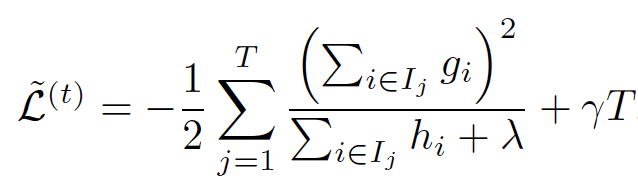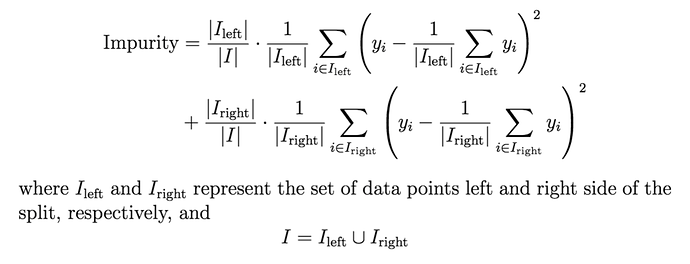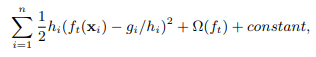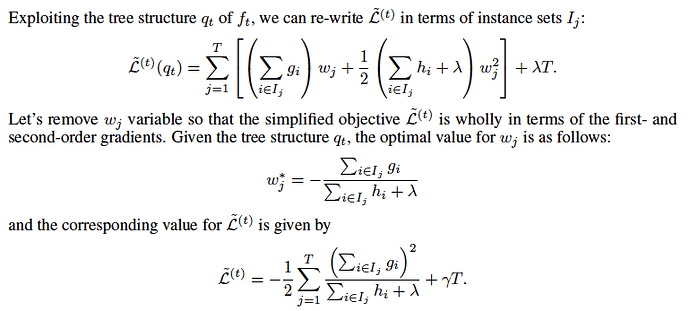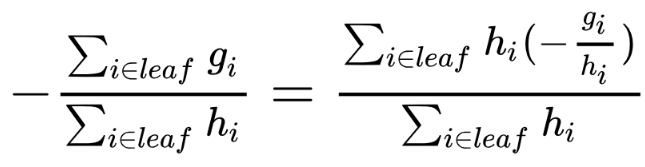Hi!
Two theoretical questions to our comminity  :
:
Question 1
I see two formulas used in context of Newton optimization method:
- x=x_0 - f’(x_0)/f’’(x_0)
- f(x)~f(x_0)+f’(x_0)(x-x_0)+1/2f’’(x-x_0)^2
From formula 2 (See original XGBoost article) we know that on each iteration of boosting RMSE with weights h_i and targets -g_i/h_i is optimized.
But direct application of formula 1 to idea of boosting just says “train weak regression model for target -g_i/h_i” which corresponds to usual RMSE optimization (not weighted!).
Are formula 1 and 2 (what is used in 2nd order boosting and XGBoost) different things?
Question 2
Is training tree on each iteration in 2nd order boosting (forget about regularization and other usuful features) the same as training regression tree in usual gradient boosting with samples x_i with weights h_i and targets -g_i/h_i?
It is easy to see that leaf weights are calculated this way - they are weighted means of values belong to each leaf.
But it seems to me that Gain in 2nd order boosting is not variance based as in normal regression decision tree.
Am I right? If yes, which tree construction strategy is better?
Thanks a lot!
Sergey.