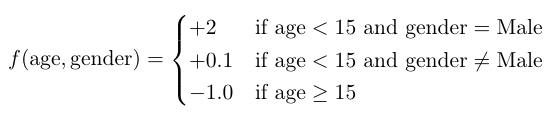I looked through Tianqi Chen’s presentation, but I’m struggling to understand the details of what the leaf weights are, and I would appreciate if someone could help confirm/clarify my understanding.
To put the equations into words on the slide “Put into context: Model and Parameters”, the predicted value/score (denoted as yhat) is equal to a sum of the K trees of the model, which each maps the attributes to scores. So far so good, I think.
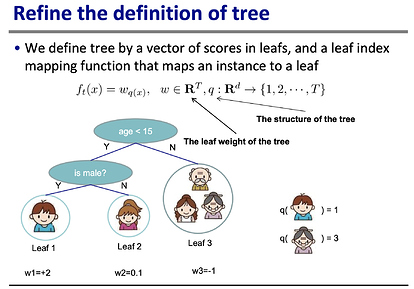
Then in this slide shown below it gives a mock example of a decision tree that calculates the amount that someone likes a computer game X. (Aside: Isn’t this a weird example? Who likes a computer game X by an amount 2? What does that even mean? Why not choose an example that has a more concrete, relatable meaning?)
Now this is where I start to get lost. I can tabulate mock data for the mock example, assuming that the model is perfect so that the weights (w1, w2, w3) are equal to the true value. But even that seems weird: what’s the difference between the predicted value and the weights?
x_i: "attributes" y_i, the true score (not yhat_i, which is the predicted score)
| |
|¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯|¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯|
| Age <15 (x_0) | is male (x_1) | Amount likes the computer game X |
| 1 | 1 | 2 | (Young boy)
| 1 | 0 | 0.1 | (Young girl)
| 0 | 1 | -1 | (Old man)
| 0 | 0 | -1 | (Old woman)
| 0 | 0 | -1 | (Young woman, older than 15)
My question is: Can someone please share what would be the ACTUAL function f? I assume it’s a vector/matrix, but what are the actual numbers? Then my bonus follow up is how would you compute the f for this mock example? I feel it’s such a simple question, but I can’t figure out the answer. If someone could break this down for me in nitty gritty detail it would be a huge help. Thanks!