Summary: I added sample weights in XGBoost training and the weights have a good dynamic range from 0.001 to above 6. However, the performance of the model only change slightly and to the wrong direction. The performance of samples with both high weights and low weights goes down slightly. I don’t have much previous experience with XGBoost model and am looking for advice on how I should approach this issue to understand the course and any possible fix.
I am using XGBoost regressor for a prediction problem. I did a 70/30 split for the available data (around 60K samples) to split training/validation. For the training portion, I used 80% to train the XGBoost and 20% to monitor the performance for early stopping. I also enforce some monotonicity constrains for further regularization of the model. I used a customized objective function which is the (log(y_pred/y_true))^2 and used abs(log(y_pred)-log(y_true)) as the evaluation metric.
In the first experiment, all the samples are equally weighted. In the second experiment, I assign different weights to the samples using the sample_weight argument in XGBRegressor.fit interface. All the other hyper-parameters are kept the same.
The expectation is for those samples with higher weights (say, top 50%), the mean error will be smaller, at the expense of increased error of lower weight samples. However, it turns out the error increases slightly for both high weight samples and low weight samples. The effect size is very small (the difference is at 4th decimal point) so the increase might not be significant. But I am still having a hard time to understand this counter-intuitive behavior.
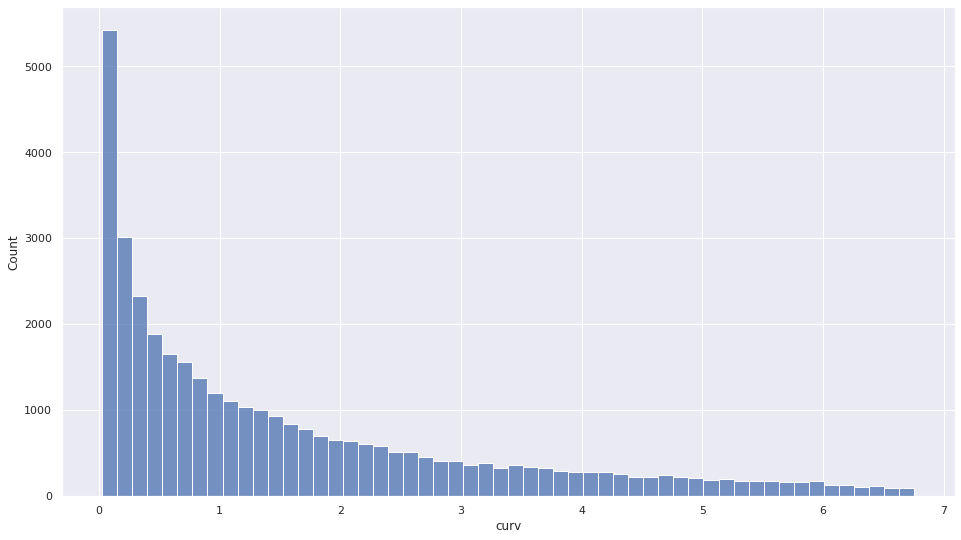
Why sample weights seems do not have much impact on model performance (and if they do, the effect is on the unexpected direction)? The weights I am using have a range from 0.02 to 6.75, but it is highly right skewed (see the plot). I am wondering if that contribute to the issue.